Part3

Maximum path sum

❓: A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Example:

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.res = root.val
        self.helper(root)
        return self.res

    def helper(self, node):
        if not node:
            return 0

        ls = max(0, self.helper(node.left))
        rs = max(0, self.helper(node.right))

        self.res = max(self.res, node.val + ls + rs)

        return node.val + max(ls, rs)

📘 💻

---

Construct Binary Tree from inorder and preorder

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder:
            return

        root_val = preorder.pop(0)
        node = TreeNode(root_val)

        root_inorder_ind = inorder.index(root_val)

        node.left = self.buildTree(
            preorder[:root_inorder_ind], inorder[:root_inorder_ind]
        )
        node.right = self.buildTree(
            preorder[root_inorder_ind:], inorder[root_inorder_ind + 1 :]
        )

        return node

📘 💻

---

Construct Binary Tree from Inorder and Postorder

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        if not postorder:
            return

        root_val = postorder.pop()
        node = TreeNode(root_val)

        root_inorder_ind = inorder.index(root_val)

        node.left = self.buildTree(
            inorder[:root_inorder_ind], postorder[:root_inorder_ind]
        )
        node.right = self.buildTree(
            inorder[root_inorder_ind + 1 :], postorder[root_inorder_ind:]
        )

        return node

💻

---

Symmetric Binary Tree

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        return self.helper(root.left, root.right)

    def helper(self, left_node, right_node):
        if left_node is None:
            return right_node is None

        if right_node is None:
            return left_node is None

        return (
            left_node.val == right_node.val
            and self.helper(left_node.left, right_node.right)
            and self.helper(left_node.right, right_node.left)
        )

📘 💻

---

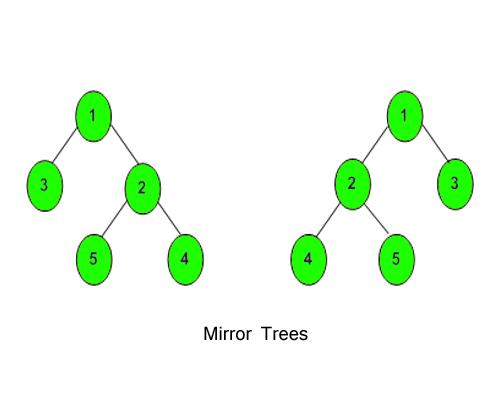
Mirror Tree

Given a Binary Tree, convert it into its mirror.

class Solution:
    def mirror(self, root):
        if not root:
            return
        root.left, root.right = root.right, root.left
        self.mirror(root.left)
        self.mirror(root.right)

💻

---

Check for Children Sum Property

❓: Given a binary tree having n nodes. Check whether all of its nodes have a value equal to the sum of their child nodes. Return 1 if all the nodes in the tree satisfy the given properties, else it returns 0. For every node, the data value must be equal to the sum of the data values in the left and right children. Consider the data value 0 for a NULL child. Also, leaves are considered to follow the property.

Example:

       35
      /  \
     20   15
    / \   / \
   15  5 10  5

Output: 1
Explanation: Here, every node is sum of its left and right child.

class Solution:
    def isSumProperty(self, root):
        if not root:
            return 1
        if root.left is None and root.right is None:
            return 1

        left = root.left.data if root.left else 0
        right = root.right.data if root.right else 0

        return (
            (1 if root.data == left + right else 0)
            and self.isSumProperty(root.left)
            and self.isSumProperty(root.right)
        )

📘 💻

---